#include <math.h>
using namespace std;
int main()
{
cout<<"\t\t\t CICLOS TERMODINAMICOS\n\nSe dice que el ciclo termodinamico es cualquier proceso \
termodinamico en los queun sistema parte de una situacion inicial y despues de aplicar estos \
procesos\nvuelve al estado original. Cuando decimos procesos termodinamicos nos referimos a la \
variacion de las propiedades termodinamicas del sistema desde un estado\ninicial a un estado final.\
\nEstos son:\n_______________________\nº 1\tCICLO OTTO º\nº 2\tCICLO DIESEL º\nº 3\tCICLO BRAYTON \
º\nº 4\tCICLO CARNOT º\nº 5\tCICLO RANKINE º \n_______________________\n";
int opcion;
cout<<"DIGITE EL NUMERO DEL TEMA: "; cin>>opcion; cout<<endl;
switch(opcion)
{
case 1:
{
cout<<" CICLO OTTO\n\n Es el ciclo termodinamico ideal que se aplica en los motores de\
combustion\n interna. Se caracteriza porque todo el calor se aporta a volumen constante.\n El motor\
Otto es un motor alternativo, esto quiere decir de que se trata de un\n sistema piston-cilindro\
con valvulas de admision y escape.\n\n ADMISION\n El piston se desplaza desde el PMS hasta el PMI. \
La valvula de admision\n se encuentra abierta. El cilindro se llena con mezcla aire-combustible. \
Al\n final de la admision la valvula se cierra.\n\n COMPRESION\n Con las valvulas cerradas, el piston\
se desplaza desde el PMI al PMS. Se\n comprime la mezcla aire-combustible. En principio esta \
compresion es\n adiabatica. Cuando el piston llega al PMS, se enciende la chispa en la bujia y se \
quema la mezcla en la camara de combustion aumentando la presion de 2 a 3.\n\n COMBUSTION\n \
Se produce la combustion de la mezcla, liberando una energia que provoca la\n expansion de los gases \
y el movimiento del piston hacia el PMI, el cual\n transmite este movimientoa la biela, y esta al \
ciguenal, desde el que se\n transmite el movimiento a las ruedas motrices mediante distintos \
sistemas, como puede ser el diferencial y las juntas homocineticas.\n\n ESCAPE\n Con la valvula de \
admision cerrada y la valvula de escape abierta, el piston se mueve hacia el PMS, expulsando los \
gases producidos durante la combustion y\n quedando preparado para empezar de nuevo el ciclo. \
En principio la presion\n dentro del cilindro es igual a la atmosferica, por lo cual el trabajo \
requerido es cero.\n________________________";
}
break;
case 2:
{
cout<<" CICLO DIESEL\n\n El motor de combustion interna Diesel se diferencia del motor de ciclo\
Otto de\n gasolina, por el uso de una mayor compresion del combustible para encenderlo, \n en vez de\
usar bujias de encendido. En el motor diesel, el aire se comprime\n adiabaticamente con una\
proporcion de compresion tipica entre 15 y 20.\n Esta compresion, eleva la temperatura al valor de\
encendido de la mezcla de\n combustible que se forma, inyectando gasoil una vez que el aire esta\
comprimido\n________________________";
}
break;
case 3:
{
cout<<" CICLO BRAYTON\n\n El ciclo Brayton, tambien conocido como ciclo Joule o Froude, se\
compone de 4\n procesos internamente reversibles: compresion adiabatica (1-2)\
suministro de\n calor a presion constante (2-3), expansion adiabatica (3-4) y cesion de calor a\
presion constante (4-1).\n\n ADMISION\n El aire frio y a presion atmosferica entrs por la boca de la turbina\n\n\
COMPRESOR\n El aire es comprimido y dirigido hacia la camara de combustion mediante un\n compresor (movido por \
la turbina). Puesto que esta fase es muy rapida, se\n modela mediante una compresion adiabatica.\n\n\
CAMARA DE COMBUSTION\n En la camara, el aire es calentado por la combustion del queroseno. Puesto que la \
camara esta abierta el aire puede expandirse, por lo que el calentamiento se modela como un proceso isobarico\n\n \
TURBINA\n El aire caliente pasa por la turbina, a la cual mueve. En este paso el aire se expande y se enfria \
rapidamente, lo que se describe mediante expansion\n adiabatica\n\n ESCAPE\n Por ultimo, el aire enfriado \
(pero a una temperatura mayor que la inicial) sale al exterior. Tecnicamente, este es un ciclo abierto ya que el \
aire que escapa\n no es el mismo que entra por la boca de la turbina, pero dado que si entra en\n la misma \
cantidad y a la misma presion, se hace la aproximacion de suponer una recirculacion. En este modelo el \
aire de salida simplemente cede calor al\n ambiente y vuelve a entrar por la boca ya frio.\n________________________";
}
break;
case 4:
{
cout<<" CICLO CARNOT\n\n Formulas\n W=n*R*(T1-T2)*Ln(Vb/Va)\n Qabs=n*R*T1*Ln(Vb/Va)\n";
cout<<" N=W/Qabs\n Donde\n w\tTrabajo\n Qabs\tCalor Absorvido\n T\tTemperatura\n V\tVolumen\n";
cout<<"________________________\n";
float W,n,R,T1,T2,a,N,Va,Vb,Qabs;
cout<<" Ingrese un valor a la variable n: ";cin>>n;
cout<<" Ingrese un valor a la variable R: ";cin>>R;
cout<<" Asigne un valor a la temperatura 1: "; cin>>T1;
cout<<" Asigne un valor a la temperatura 2: "; cin>>T2;
cout<<" Ingrese el volumen a "; cin>>Va;
cout<<" Ingrese el volumen b "; cin>>Vb;
a=(log(Vb/Va)/log(10));
W=n*R*(T1-T2)*a;
Qabs=n*R*T1*a;
N=W/Qabs;
cout<<"EL TRABAJO REALIZADO ES: "<<W<<endl; cout<<"EL CALOR ABSORVIDO ES: "<<Qabs<<endl;
cout<<"EL RENDIMIENTO ES: "<<N<<endl;
}
break;
case 5:
{
cout<<" CICLO RANKINE\n\n FORMULAS:\n Qent=(h1-h4)*m:\n Qsal=(h2-h3)*m\n Wturb=(h1-h2)*m\n";
cout<<"Wbomb=(h4-h3)*m\n N=(Wturb-Wbomb)/Qent\n Donde:\n Qent\t\tPOTENCIA TERMICA DE ENTRADA\n";
cout<<"Qsal\t\tPOTENCIA TERMICA DE SALIDA\n Wturb\t\tPOTENCIA MECANICA DE LA TURBINA\n";
cout<<"Wbomb\t\tPOTENCIA MECANICA DE LA BOMBA \n h1,h2,h3,h4\t\tENTALPIAS\n";
cout<<"m\t\tCAUDAL MASICO\n_____________________\n";
int m;
float h1,h2,h3,h4,Wturb,Wbomb,Qent,Qsal,N;
cout<<"INGRESE LA ENTALPIA 1\t";cin>>h1; cout<<"INGRESE LA ENTALPIA 2\t";cin>>h2;
cout<<"INGRESE LA ENTALPIA 3\t";cin>>h3; cout<<"INGRESE LA ENTALPIA 4\t";cin>>h4;
cout<<"INGRESE LA MASA ";cin>>m;
if (m!=0)
{
Qent=(h1-h4)*m; Qsal=(h2-h3)*m; Wturb=(h1-h2)*m; Wbomb=(h4-h3)*m; N=(Wturb-Wbomb)/Qent;
cout<<"LA POTENCIA TERMICA DE ENTRADA ES: "<<Qent<<endl;
cout<<"LA POTENCIA TERMICA DE SALIDA ES: "<<Qsal<<endl;
cout<<"LA POTENCIA MECANICA DE LA TURBINA ES: "<<Wturb<<endl;
cout<<"LA POTENCIA MECANICA DE LA BOMBA ES: "<<Wbomb<<endl;
cout<<"EL RENDIMIENTO TERMICO DEL CICLO ES: "<<N<<endl;
}
else
{
cout<<"Indeterminado INGRESE UN VALOR m<>0"<<endl;
}
cout<<"*****************************"<<endl;
}
break;
}
cout<<endl<<endl;
system("pause");
return 0;
}
https://drive.google.com/file/d/0B3RZqyBWldi1YkV4Ri1MMkJFX1k/view?usp=sharing

































 , como una variable de estado cuya variación en un proceso adiabático es el trabajo intercambiado por el sistema con su entorno:
, como una variable de estado cuya variación en un proceso adiabático es el trabajo intercambiado por el sistema con su entorno:

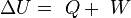
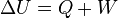
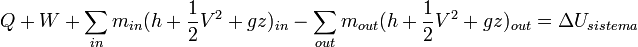

 es la energía por unidad de masa del flujo y comprende la
es la energía por unidad de masa del flujo y comprende la 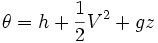


 , por lo que el balance de
, por lo que el balance de 